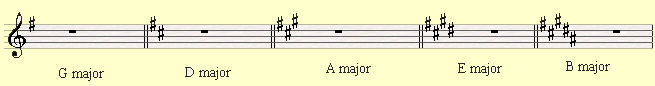The Circle of Fifths
Home » Piano Theory » Circle of Fifths
A KEY SIGNATURE states the sharp, flat, or natural signs placed at the beginning of a staff indicating the tonality of the composition. In other words it tells us how many sharps or flats are used in a piece.
As a starting point we'll have to agree what makes musical keys closely related?
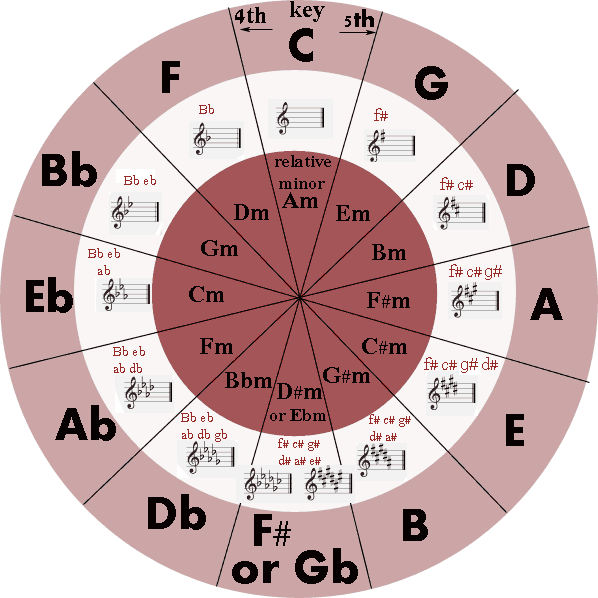
The circle of fifths was build to help us visualize the relationship between the different major and minor keys in order to allow us to identify and remember the order of sharps and flats in key signatures and find related musical scales.
"I found your explanations of piano theory clear and to the point."
Well, you might have assumed that adjacent keys would be related but this is not the case. If you'll take a quick look at the circle of fifths you'll see that related keys are having similar key signatures (almost the same number of sharps and flats).
Why is it Called the Circle of Fifths?

Well, it turns up that when you go from one key to the closest related key you basically go up or down by an interval of a perfect fifth. An interval of a perfect fifth is when you go 3 1/2 tones up or down from a certain key.
Intervals can also be inverted. That means that you could take an interval and turn it upside down so that the lower note will be raised and become the upper note of the interval and so you could refer the counter-clockwise direction of the circle of fifths as a "circle of fourths".
We'll take C major as an orientation point since it has no sharps and flats. As you go clockwise around the circle of fifths, the notes move in perfect 5ths.
Going up for C major in the circle of fifths (clockwise) will increase the number of sharps in the next related key.
Going down from C major in the circle of fifths will increase the number of flats in the next related key (Or decrease the number of sharps).
An Example
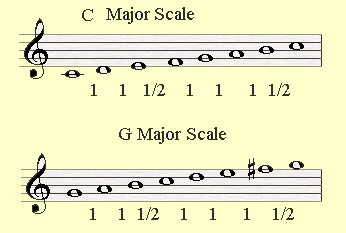
Well, C major is a diatonic scale, meaning that it is built from the formula of 1,1,1/2,1,1,1,1/2. So are the rest of the major and natural minor scales.
A C major scale could be easily formed by playing only the white keys starting from C to the higher C. They naturally fit in the formula of the diatonic scale. Therefore the key signature of C major has no sharps and flats.
If we go to the next slice of the circle (clockwise) we'll see that G major is the closest related key since its key signature has only one sharp. When we'll form the formula of the diatonic scale starting from G we will see indeed that F sharp was replaced with F.
Exercise 1
1. What are the keys most closely related to E flat major? To A minor?
Exercise 2
2. Name the major and minor keys for each key signature.

The Order of Adding Sharps and Flats in the Circle
If you ask yourself how you could remember which sharps and flats each keys has,
let me tell you that there's a simple logic to do that as well.
If G major has F sharp added, the next related key (D) will have C
sharp which is located a perfect fifth above F sharp.
The perfect fifth above C sharp is G sharp so A major scale would have F sharp, C sharp and G sharp in its key signature.
Bottom line,Each sharp and flat that is added to a key signature is also a perfect fifth away from the last sharp or flat that was added.
Exercise 3
3. According to what we've learned, G major has one sharp (f#). Name the next four sharps keys we're going to add as we move clockwise in the circle in the order they're added?And which scale gets each sharp?
What's the connection between the major keys and the minor keys?

Each major key has its parallel minor key. That means that they share the same notes.
In fact if you take a major key and starting playing it from its
SIXTH NOTE you'll be playing its parallel minor key.
The parallel minor keys have their sharps added in the same order as the major keys.
If you'll take Am minor for example, it has no sharps. As you go as slice to the
write you'll be adding F sharp to the next minor sclae, E minor.
E minor is indeed the parallel minor of G major (Who has F sharp in it as well).
Exercise 4
4. If E minor has one sharp, could you state according to the information the next four minor scales. Could you tell me which sharp is added to each scale?
How Can I Use the Circle of Fifths in a Practical Manner?
The circle of fifth was being created in order to supply a logical manner to define tuning in a more exact way in the past.
Today we use in order to quickly tell between the different key signatures and in order to modulate or transpose the different keys.
When you modulate you basically move from one key to a relative key in a convincing manner (more about that soon...)
The more closely related is the key the easier it is to modulate to it.
TRANSPOSING is when you take a piece or song and you want to play it in another key that fits you needs. (Singers often want to sing higher or lower then the chosen key if they wake up happy or their throat soars. :-)
Those of us who are proficient in the secrets of the circle could easily transpose a musical piece without any effort (unless the new key contains six flats or so which is often annoying and then someone (the singer or the piano player) has to compromise).
Exercise 5
5.After B flat major, name the next four flat keys, and name the flat that is added with each key.

The circle of fifths helps you to know which scale you're in and actually you can use it to recognize common chord progressions?
In order to get the full potential of what you've learned here you should go through the Rocket Piano Ultimate Learning kit. With Rocket Piano you'll learn to implement the theoretical knowledge you acquired in here and exercise it in order to play more smoothly, improvise and best of all - You'll learn to play piano by ear.
Click here to check out the Rocket Piano Learning Kit Now!