The Whole Tone Scale
Home » Piano Theory » The Whole Tone Scale
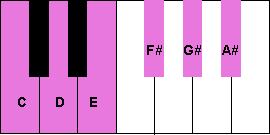

This scale divides the octave into six whole tones.
Therefore the distance between each note and its neighbor in the scale would be a whole step.
The scale is very different from the major and minor scales since it lacks the contrast created by the semi-tones in these scales.
Therefore this scale sounds kind of spacey and is often interpreted in music as a dreamy or mysterious scale.
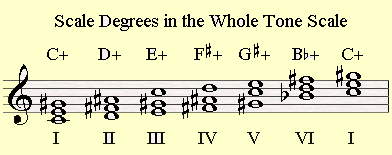
If we're going to build chords upon the six scale degrees of the scale we'll realize they're all augmented. Notice that all thirds are a major and that there is no stable fifth in the scale (a perfect fifth).
The fact there isn't a perfect fifth in the scale abolishes the basic tension and release existing in a diatonic scale
where the fifth lease to the tonic (harmonically speaking).

Since there are only whole tones in the scale, only two scales exist in the whole tone structure. Your starting point will set the tonic of the scale and will be based upon repetitions and melodic emphasis.
In the late 19th a decline in the functionality of harmony started. The scale was used often then since it has a vague functionality.
There are some magnificent piano pieces written with this scale.
Check out the introduction to "You are the Sunshine of my Life" by Stevie Wonder for example.

Claude Debussy used the scale quite a lot. Here's a beautiful prelude of him where he create a lot of beauty only from the whole tone scale.















